雪球的威力

今天想討論一下複息增長的威力。

什麼是複息，為何必須盡早開始投資？

讓我在這裡簡單解釋一下複息是什麼。

現在給大家一條數學選擇題，今天投資年1元，每年回報為10%，20年後這個1元會變成怎麼樣？

A) $1 x (1+10% x 20) = $3

B) $1 x (1+10%)^20 = $6.7

答案是B

答案A及B的分別就是一個是單利息，一個是複利息。相差竟達1倍。如果我們將時間點拉長多10年，兩者的回報分別為

A) $1 x (1+10% x 30) = $4

B) $1 x (1+10%)^30 = $17.45

兩者相差達4倍多。

從以上的算式，我們知道複利的效果會隨著時間倍增，效果會隨時間增長而變得十分明顯。我相信網上有其他投資師兄對複息有更詳細的講解，我在這裡就不再長篇大論的解說了。

如果在看這篇文章的你是20歲還未到的年青人，恭喜你，雖然你未必有很大的本金，但你有我們沒有的青春、時間。可以完全發揮複利的威力。

以下是答案A及答案B分別的投資策略：

答案A：每年提出當年的利潤，讓本金去滾存。
答案B：不提出當年利潤, 讓本金及利潤繼續滾存。

聰明的你，一定會選擇答案B的投資策略吧!

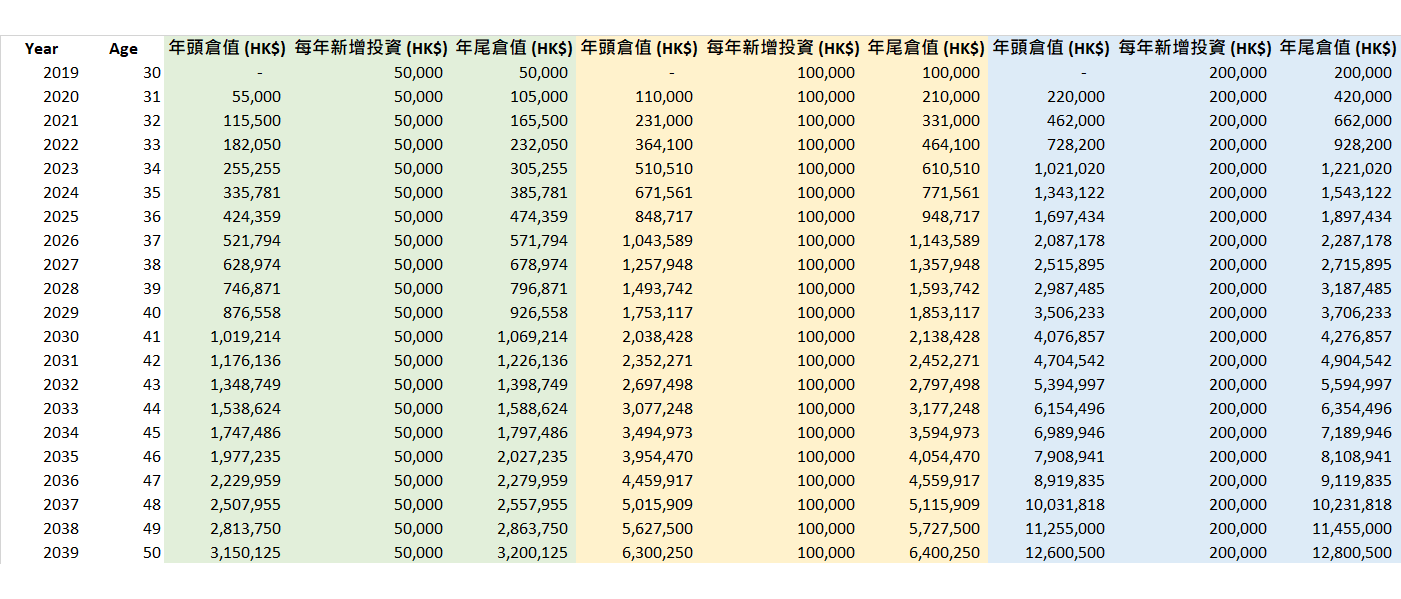
現在我們去做一個假設，用數字量化效益。分別每年固定投資HK$50K，HK$100K及HK$200K，年回報平均為10%， 20年後組合的價值：

20年後投資組合的價值分別變成大約HK$3.2M，HK$6.4M及HK$12.8M。

作為一個年輕人，我明白一下子不可能每年投入大量的資本。

那我們就把每年的投資額減去一個零，即每年分別投資HK$5,000、 HK$10,000及HK$20,000。這個數字困難嗎？

絕對不難。如果我們將這個數字按月平分，即每月需要儲約HK$417、HK$833及HK$1,667。

只要我們減少開支，包括出外用餐的次數或買不必要的東西，其實已經可以儲下這筆金額了。我不是要求大家完全不消費，如果因為儲錢而犧牲了生活，令自己的生活變得乏味，社交圈子減少，這是不正確的。適度的消費是應該的。

隨著我們在工作場上晉升，工資也有增長的機會。我們可以增加每月可動用的投資額。加快整個資產增值得過程。

這篇文章除了希望大家了解複利息的威力外，還希望各位能明白時間對於我們資產增值的重要，盡早開始投資。年青人，加油吧！